Par : Jesse Rogerson, Ph.D.
Ingenium – Musées des sciences et de l’innovation du Canada
M’imaginer astronaute fait partie de mon travail
Crédit photo
Ingenium
Jesse l’astronaute fait de l’exploration sur Encelade
Comme conseiller scientifique du Musée de l’aviation et de l’espace du Canada, j’ai l’occasion de travailler à des projets vraiment très amusants. Récemment, j’ai contribué aux aspects scientifiques d’un jeu vidéo sur le thème de l’espace appelé OrbiBlox inc., que nous venons de lancer pour console Nintendo Switch. (Vous ne saviez pas que les musées développaient des jeux vidéos? Eh oui! Nous sommes branchés à ce point-là. Jetez un coup d’œil à nos jeux et applications.)
OrbiBlox inc. est à la fois un jeu de casse-tête et un jeu de combat, où les joueurs livrent des marchandises à travers le système solaire. Pour chaque planète, lune et astéroïde visités, la gravité et les obstacles environnementaux sont réalistes. Par exemple, Io comporte des coulées de lave : cette lune de Jupiter est le corps céleste dont l’activité volcanique est la plus élevée de notre système solaire.
Pendant mes recherches préliminaires, j’ai dû me poser une question intéressante : sur Encelade, les geysers seraient-il assez puissants pour soulever un humain?
La réponse, malheureusement, est non… sauf avec un peu de créativité. Mais avant d’aller plus loin, examinons certaines données.
Encelade est une lune de Satune dont le diamètre est de 500 km (beaucoup moins que le diamètre de la plus grosse lune de Saturne, Titan, qui atteint les 5 000 km). Encelade n’a pas d’atmosphère, et sa surface est entièrement couverte de glace d’eau. Un gigantesque océan d’eau se trouve sous cette glace, à de nombreux kilomètres de profondeur.
Ce qui est plus directement lié à ma question, c’est le fait qu’au pôle Sud d’Encelade, un énorme réseau de geysers crache de la vapeur d’eau, des molécules complexes et autres choses encore dans l’espace. Comme la surface d’Encelade est craquée et fissurée, l’eau liquide de l’océan enfoui est exposée au vide de l’espace, qui la transforme rapidement en gaz (vapeur d’eau), qui s’échappe immédiatement. Ce phénomène crée d’immenses panaches de vapeur d’eau visibles de très loin.
Crédit photo
Prise par la sonde spatiale Cassini, cette image montre les geysers d’Encelade.
Les gaz qui s’échappent de la glace fissurée d’Encelade forment des panaches de centaines de kilomètres de hauteur dans l’espace. En fait, leur ampleur est telle et ils contiennent tant de matière qu’Encelade a formé un anneau complet autour de Saturne : l’anneau E.
Crédit photo
Prise par la sonde spatiale Cassini à une distance de plus de 2 millions de kilomètres, cette image montre l’alimentation, par les geysers, d’un anneau géant et diffus appelé anneau E.
Examinons maintenant ma question de départ : si j’étais astronaute, sur la surface d’Encelade, et que je sautais dans les craques qui laissent échapper ce gaz, le vent serait-il suffisant pour me soulever et me projeter dans l’espace?
Cette question est en fait assez simple à résoudre, car il n’y a que deux forces à tenir en compte : celle de la gravité et celle du vent. Logiquement, si la force gravitationnelle d’Encelade est supérieure à la force du vent, je resterai les deux pieds sur la glace. Mais dans le cas contraire, je serai projeté dans l’espace, jusqu’à l’anneau E de Saturne.
Résumons.
La force gravitationnelle est facile à calculer; un obscur savant* l’a compris il y a plus de 300 ans. L’équation est la suivante :
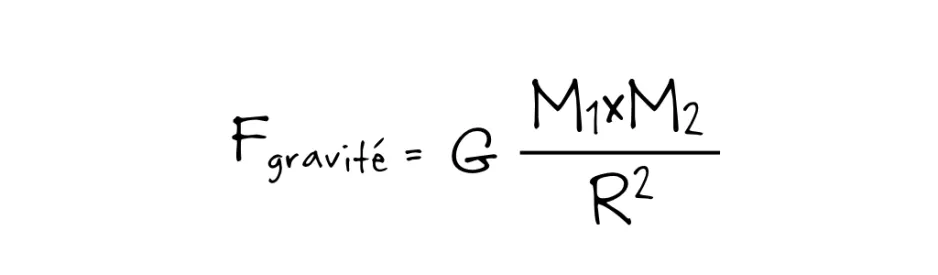
Où G est la constante de la gravitation universelle, M1 est la masse d’Encelade (soit environ 1E22 kg, ou 10,000,000,000,000,000,000,000 kg), M2 est la masse de Jesse l’astronaute (soit environ 75 kg), et r est la distance entre le centre d’Encelade et la surface, où se trouve le brave explorateur que je suis (soit le rayon d’Encelade : 250 km). La force gravitationnelle qui agirait sur moi se calculerait donc ainsi :
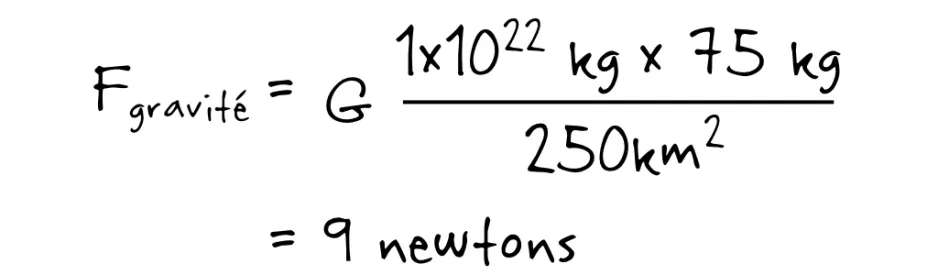
[Aside: 9 newtons? Pas plus? La Terre exerce sur Jesse le non-astronaute une force d’environ 735 newtons (lorsque je suis sur la surface). Encelade est vraiment toute petite!]
Selon ce calcul, les geysers d’Encelade doivent exercer une force de plus de 9 newtons sur Jesse l’astronaute pour le soulever. Mais comment calculer la force du vent? C’est tout simple : il existe une formule pour ça aussi!
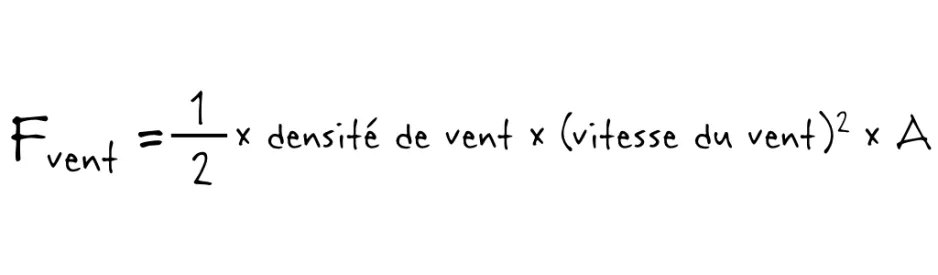
Où A correspond à l’espace que j’occupe dans le vent, puisque la force du vent sur mon corps dépend de l’espace que j’occupe : plus j’occupe d’espace, plus mon corps bloque de vent. J’estime que j’occupe environ 0,85 mètres carrés (= 1,7 m * 0,5 m). Les seules autres inconnues dans cette équation sont la vitesse du vent et sa densité (combien de particules de vent par mètre cube). Comme je ne suis pas un expert des geysers d’Encelade, je ne savais pas où chercher cette information. J’ai donc envoyé un courriel à mon ami John Moores, Ph. D., l’une des personnes les plus intelligentes que je connaisse. Il m’a suggéré de sources fiables, et j’ai appris que les vents qui sortent des geysers d’Encelade ont une vitesse de vent est 300 m/s et que la densité estimée de leur panache est 0,00000002 kg / m3 (1,225 kg/m3 est la densité de notre atmosphère au niveau de la mer).
Donc, voici ce que l’on obtient en mettant ces données dans l’équation.
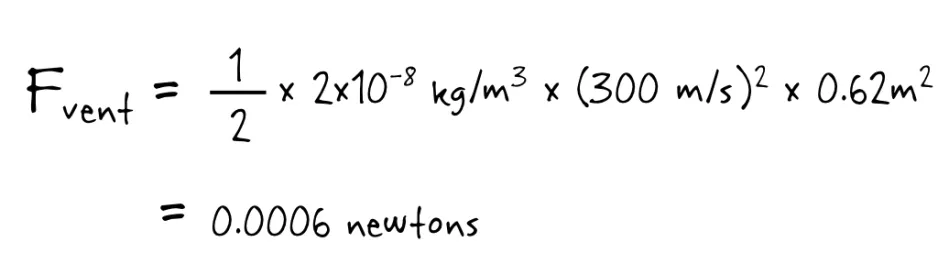
[Aside: 300 m/s!? C’est fou! La vitesse d’une auto sur la transcanadienne est d’environ 30 m/s. Les geysers crachent leur eau 10 fois plus vite que la vitesse d’une auto sur l’autoroute! Évidemment, ce n’est pas seulement une question de vitesse : il faut aussi tenir compte de la force de la masse sur l’objet qui se déplace, de là l’importance de la densité.]
Le vent exercerait une force de 0,0006 newton sur moi. C’est évidemment beaucoup moins que la force gravitationnelle d’Encelade, donc bien insuffisant pour me soulever (*trombone triste*). Je suis un peu déçu : honnêtement, j’espérais pouvoir sauter dans le geyser et flotter comme dans un simulateur de chute libre.
Heureusement, mon ami John a trouvé une façon beaucoup plus divertissante d’utiliser ce résultat. Si le vent exerce une force insuffisante sur la toute petite surface de 0,85 m2 que j’occupe, quelle surface devrais-je occuper pour contrebalancer 9 newtons de gravité? Pour le savoir, il suffit de renverser la formule précédente.
La réponse approximative est de 12 000 m2. À quoi correspond une surface de 12 000 m2? À un cercle dont le rayon est de 60 m, ou à environ 2 terrains de football**, 7 patinoires de la LNH ou la colline parlementaire. Je n’ose même pas penser aux tests nécessaires pour mettre à l’épreuve un parachute aussi grand. En tous cas, en principe, on pourrait fabriquer un parachute de cette taille, l’emporter sur Encelade et chevaucher ses panaches. Évidemment, la valeur scientifique d’une telle expérience est douteuse, mais après tout, je ne me suis pas fait astronaute de bande dessinée pour publier des articles savants, mais bien pour la gloire!
* Sir Isaac Newton… Ça vous dit quelque chose?
** selon le règlement de la LCF, évidemment
Jesse Rogerson, Ph.D.
Jesse est un scientifique, un éducateur et un communicateur scientifique passionné. En tant que professeur adjoint à l'Université York, au département des sciences, de la technologie et de la société, il enseigne trois cours : Histoire de l'astronomie, Introduction à l'astronomie et Exploration du système solaire. Il collabore fréquemment avec le Musée de l'aviation et de l'espace du Canada, et prête sa voix d’expert au Réseau Ingenium. Jesse est un astrophysicien et ses recherches explorent la façon dont les trous noirs supermassifs évoluent à travers le temps. Que ce soit en classe, par le biais des médias sociaux ou à la télévision, il encourage les conversations sur la façon dont la science et la société se croisent et sur la raison pour laquelle la science est pertinente dans notre vie quotidienne.
