Canada Aviation and Space Museum
Astronaut fantasies are part of my job description
Photo Credit
Ingenium
Astronaut Jesse investigating things on Enceladus.
As the Science Advisor for the Canada Aviation and Space Museum, I get to work on some really fun projects. Recently, I helped out with the science behind a space-themed video game we just released on the Nintendo Switch called StarBlox Inc (you didn’t know that museums made video games? We do! We’re cool like that...check out our games and apps).
StarBlox Inc. is a puzzle-brawler mashup where players travel around the solar system delivering cargo. Each of the planets, moons, and asteroids you visit has appropriate gravity and environmental challenges. For example, we have lava flows on Io (a moon of Jupiter, and the most volcanically active object in the solar system).
An interesting question came up during my background research: would the water geysers of Enceladus be strong enough to lift a human off the ground?
The answer, unfortunately, is no…. UNLESS you get creative! But let’s step back a minute and get some background.
Enceladus is one of Saturn’s moons. It’s about 500 km in diameter (much smaller than Saturn’s largest moon, Titan, which is about 5,000 km wide), has no atmosphere, and has a surface covered entirely in water ice. Many kilometres below that ice, there’s a massive ocean of water.
More pertinent to my original question, at the south pole of Enceladus, there’s a massive network of geysers launching water vapour, complex molecules, and other stuff into space. Cracks and fissures in the surface ice of Enceladus exposes the liquid water from the ocean below to the vacuum of space, allowing it to quickly escape in gas form (water vapour). This results in massive plumes of water vapour visible from afar:
Photo Credit
Taken by the Cassini Spacecraft, this image shows the water geysers of Enceladus.
The cracks in the ice of Enceladus are venting gas hundreds of kilometres into space! In fact, the plumes are so big and release so much material that Enceladus has created an entire ring around Saturn: the E ring.
Photo Credit
Taken by the Cassini Spacecraft from over 2 million kilometres away, the image shows the water geysers feed into a giant defuse ring known as the E-ring.
Now back to the original question: if I was an astronaut walking around the surface of Enceladus and I jumped into the cracks that are venting the gas, would the wind be able to lift me up and launch me into space?
This is actually a pretty simple question because there are only two forces I need to worry about: the force of gravity, and the force of the wind. Logically, if the gravity of Enceladus pulls downward with a stronger force than the upward force of the wind, then I’ll stay on the icy surface of Enceladus. If the opposite is true, then I’ll be blown away to join the E ring of Saturn.
So it boils down to:
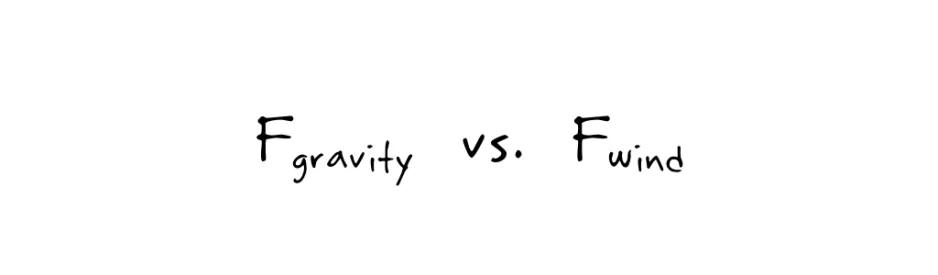
The force of gravity is easy to calculate; some no-name scientist* figured it out over 300 years ago. The equation is:
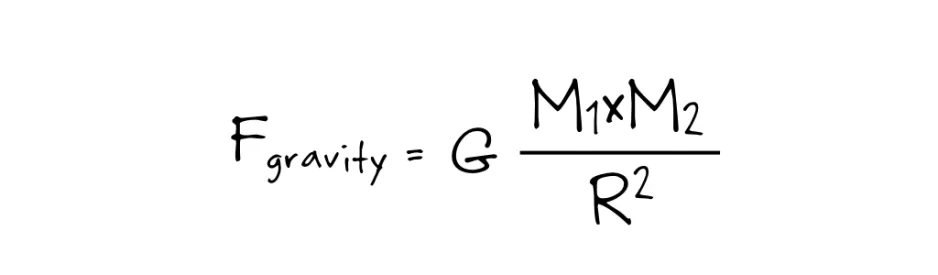
Where G is the Universal Gravitational Constant, M1 is the mass of Enceladus (which is roughy 1E22 kg, or 10,000,000,000,000,000,000,000 kg), M2 is the mass of Astronaut Jesse (which is roughly 75 kg), and R is the distance from the centre of Enceladus (since I’m standing on the surface, like the brave explorer that I am, that distance is just the radius of Enceladus: 250 km). Doing the math, that means the force of gravity on me would be about:
[Aside: 9 newtons? That’s it? The Earth pulls down on non-Astronaut Jesse with about 735 newtons of force (when I’m standing on the surface). Wow… Enceladus is a small place!]
That means the geysers of Enceladus need to exert more than 9 newtons of force on Astronaut Jesse in order to lift him up. So how do we calculate the force of wind? There’s a formula for that too!
Where A is how much area I take up in the wind, this is because the force of the wind on my body depends on how much space I take up; the larger I am, the more of the wind I catch with my body. I estimate I’m about (1.7m x 0.5m=) 0.85 square metres. The only other unknown values in this equation then are the velocity of the wind, and the density of the wind (how many particles of wind per cubic metre). And since I’m not an expert on the geysers of Enceladus, I didn’t know where to look for this information. So I emailed my friend Dr. John Moores (who’s one of the smartest people I know). He pointed out some good resources for me and I learned that the geysers on Enceladus travel at a velocity 300 m/s and have an estimated density of the plume is 0.00000002 kg / m^3 (where as the density of our atmosphere at sea level is 1.225 kg/m^3).
So plugging the values into the equation:
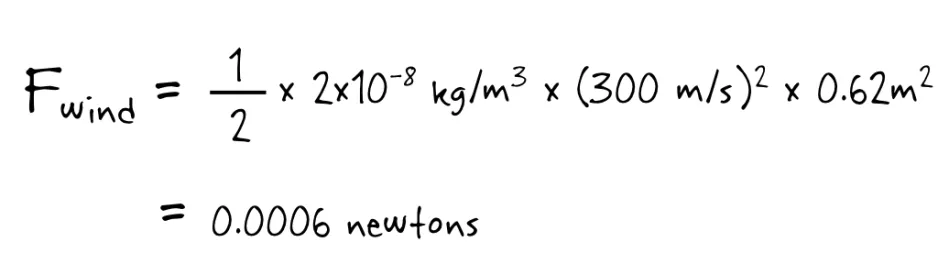
[Aside: 300 m/s!? That’s insane! A car on the TransCanada Highway will be travelling only about 30 m/s. The geysers are shooting water out 10 times faster than a car on the highway! Though it’s not just about the speed, it’s about the force applied by the mass of the moving object, which is where the density comes into the equation.]
The wind would exert 0.0006 newtons on me. Clearly, that’s much less than the force of Enceladus’ gravity, and thus not nearly enough to lift me up (*sad trombone*). Honestly, I’m a little disappointed; I had hoped that I would be able to jump into the geyser and float like an indoor skydiver.
But luckily, Dr. John had a much more entertaining way of looking at this result. If the wind isn’t exerting a strong enough force on my measly 0.85m^2, then what surface area would I need to take up to match the 9 Newtons of gravity? We can flip the above equation to figure it out:
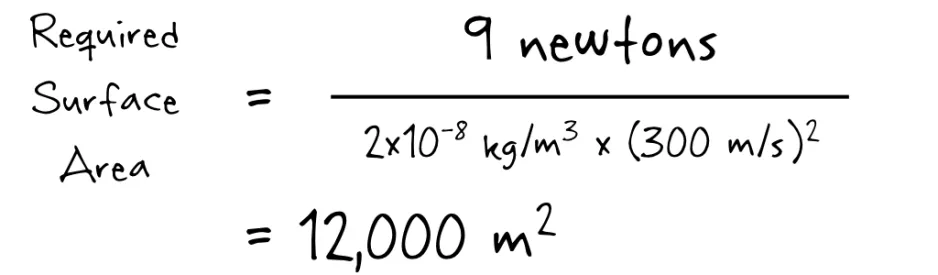
The answer is, roughly, 12,000 m^2!
How big is that? Well, 12,000m^2 is equal to a circle with a radius of 60 m, or roughly two football fields**, or seven NHL hockey rinks, or the size of Parliament Hill (... I can’t even imagine the testing that would be needed for a parachute of that magnitude). Anyway this means, in principle, one could construct a parachute of this size, bring it to Enceladus, and ride the plumes! Of course, the scientific value of this is questionable, but I didn’t become a cartoon astronaut for the publications, I became one for the fame.
* Sir Isaac Newton… have you heard of him?
** CFL regulation, of course
Jesse Rogerson, PhD
Jesse is a passionate scientist, educator, and science communicator. As an assistant professor at York University in the Department of Science, Technology, and Society, he teaches three classes: History of Astronomy, Introduction to Astronomy, and Exploring the Solar System. He frequently collaborates with the Canada Aviation and Space Museum, and lends his expert voice to the Ingenium Channel. Jesse is an astrophysicist, and his research explores how super massive black holes evolve through time. Whether in the classroom, through social media, or on TV, he encourages conversations about how science and society intersect, and why science is relevant in our daily lives.
